Волшебный алгоритм для детей , как вывести и вспомнить таблицу умножения.

В возрасте 7-9 лет каждый ребенок сталкивается с известным обрядом начальной школы — изучение таблицы умножения. Как же сложно бывает объяснить ребенку, что таблицу умножения нужно выучить, она точно пригодится в будущем. Ребенок спокойно справляется с запоминанием таблицы до цифры 5 , а вот с цифрами 6, 7, 8 и 9 — становится уже труднее.
Но что, если сделать изучение таблицы умножения с этими цифрами занимательным и даже волшебным? Ведь в числах скрыто очень много магии, и  если использовать алгоритмы , которые в них скрыты, получается, как будто бы, заклинание. Мы покажем вам, как превратить обычную “зубрёжку” в вычислительное колдовство.

Алгоритм — шпаргалка

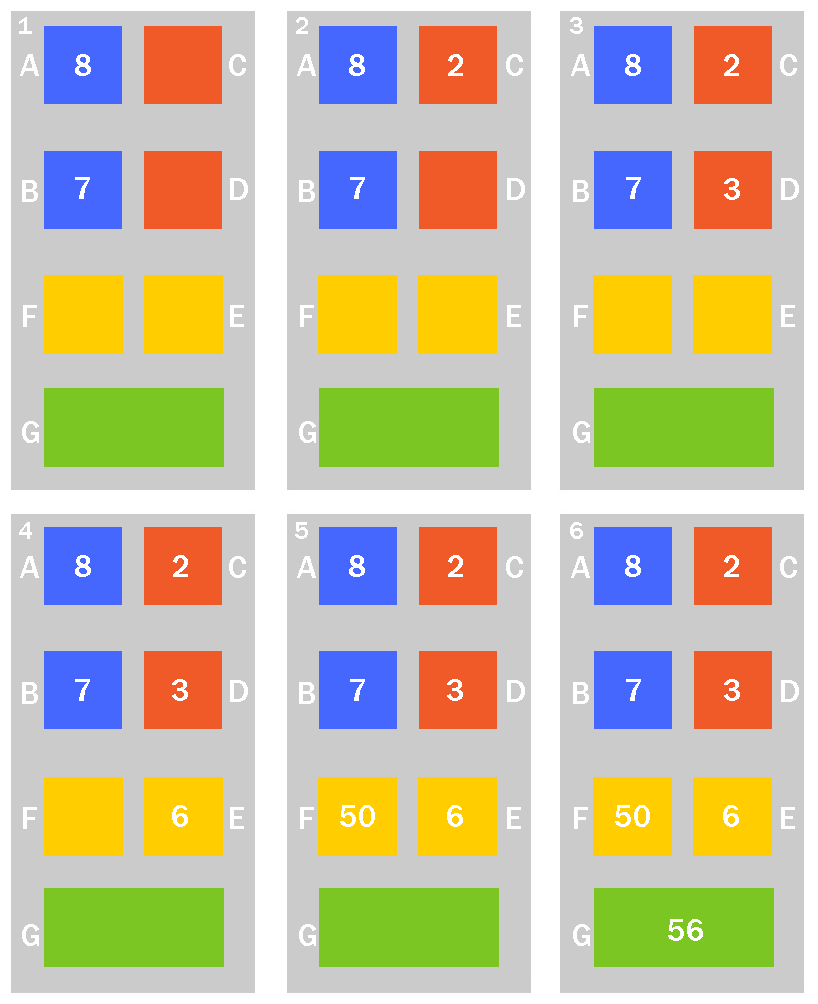
Предположим, у вас есть два из этих противных старших числа, которые нужно умножить, например, 8 × 7.

1. Нарисуйте 7 полей с метками A, B, C, D, E, F и G, или воспользуйтесь нашим шаблоном. Напишите одно из чисел, которое вы хотите умножить, в поле A, а другое — в поле B.
   • например, если вы хотите рассчитать 8 x 7, поместите 8 в поле A и 7 в поле B.
2. Вычтите число в поле A из 10 и напишите ответ в поле C.
   • 10-8 = 2, поэтому напишите 2 в поле C.
3. Вычтите число в поле B из 10 и поместите ответ в поле D.
   • 10-7 = 3, поэтому напишите 3 в поле D.
4. Умножьте два числа в ячейках C и D вместе. Поместите ответ в поле E.
   • 2 х 3 = 6, поэтому мы пишем 6 в поле E
   • Обратите внимание, ваши числа: A и B были выше 5, новые, которые вы должны умножить вместо этого, будут ниже 5, так что это очень просто.
5. Теперь вычтите число в блоке C из блока B (они находятся по диагонале) и умножьте ответ на 10 (просто добавьте ноль в конце), записав ответ в блоке F.
   • 7-2 = 5, а теперь умножаем это число на 10 и записываем 50 в блоке F.
6. Теперь посчитаем ответ в блоке G, добавив число в блоке F к числу в блоке E.
   • В блоке E записано 50, а в F, 6, получаем 50 + 6 = 56 , что является ответом на исходное умножение (8 × 7).

Попробуйте этот алгоритм самостоятельно, например на числах: 6 × 9, 7 × 6 и 8 × 9.

Этот вычислительный алгоритм похож на колдовство! Но всегда ли он выдает правильный ответ? Конечно, мы уверены, что вы нам доверяете. Но мы решили, что все таки должны доказать вам (или, по крайней мере, привести строгие аргументы), что алгоритм действительно всегда работает.

Доказательство

ШАГ 1:  Давайте назовем цифру в поле A — “a”, цифру в поле B — “b” и так далее. Мы пытаемся найти ответ на умножение ab или a * b.

Теперь (см. на рисунок ниже) вместо непосредственно умножения значений, мы постараемся вывести его с помощью уравнений.

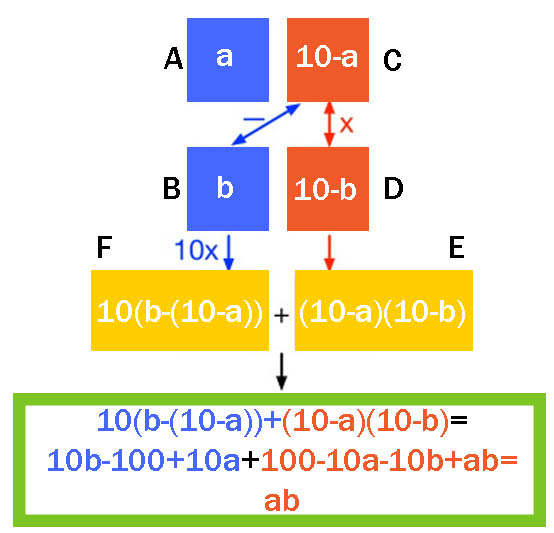
ШАГ 2: с = 10-а

ШАГ 3: d = 10-b

ШАГ 4:  е = (10-а) (10-b).
Чтобы получить число в ячейке E , мы должны перемножить числа С и D между собой.

ШАГ 5: f = 10 (b- (10-a))
Чтобы получить число F мы должны вычесть из числа B — число С и умножить разность на 10

ШАГ 6: g = 10 (b- (10-a)) + (10-a) (10-b)
А теперь складываем числа E и F , чтобы получить окончательный ответ.

g = 10 (b- (10-а)) + (10-а) (10-b)

Раскрываем левые скобки последовательно:

= 10 (b-10 + а) + (10-а) (10-b)

= 10b -100 + 10a + (10-a) (10-b)

А теперь перемножаем правые скобки:

= 10b -100 + 10a + 100 -10a -10b + ab

А теперь, упрощаем выражение.

= 10b + 10a -10a -10b + ab

= 10a -10a + ab

= ab

Итак, теорема даказана. В результате наших математических преобразований мы получаем исходное произведение: A * B

Обязательно познакомьте своего ребенка с этим алгоритмом. Ведь в этом случае скучное домашнее задание по математике превратится в занимательную волшебную игру). Кроме того, если он когда — нибудь забудет произведение больших чисел, он всегда сможет вывести их , с помощью этой формы — подсказки.

Полезные ссылки

1. Больше информации о данном алгоритме: https://teachinglondoncomputing.org/tudor-computational-witchcraft/
2. Головоломки для обучения детей двоичной системе счисления